[2018] 추석 트래픽

처리량의 변화가 어디서 일어나는지 알아내는 것에 어려움이 있었다. 큰 문제를 작은 문제로 나누어 풀어나간다는 것에 초점을 두고 하나의 로그데이터를 살펴보았을 때 어디서 처리량의 변화가 일어나는지 확인하였다. 이 과정에서 시간이 정말 오래걸렸다.
문제 설명
1. 추석 기간인 9월 15일 로그 데이터를 분석한 후 초당 최대 처리량을 계산하여 초당 최대 처리량을 리턴한다.
2. 입력 : hh:mm:ss.sss T
  - hh : 시
  - mm : 분
  - ss : 초
  - sss : 0.sss초
  - T : 처리시간(2s, 0.312s)
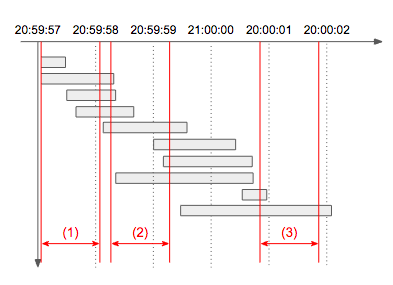
(1)에서의 처리량 : 4 (2)에서의 처리량 : 7 (3)에서의 처리량 : 2
문제 풀이

예제
입력: [ 2016-09-15 01:00:04.001 2.0s]
01:00:04.001 이전의 처리량 : 0
01:00:04.001 ~ 01:00:06.001 까지의 처리량 : 1
01:00:06.001 이후의 처리량 : 0

- 위와 같이 로그데이터의 양끝에서 처리량의 변화가 일어난다.
- 모든 로그데이터의 start를 기준으로 왼쪽으로 1초 동안에 처리량을 구하여 그 중에서 가장 큰 처리량을 리턴한다.

#include <string>

#include <vector>


using namespace std;

struct node
{
	int start;
	int end;
};

int max(int a, int b)
{
	return a < b ? b : a;
}

int solution(vector<string> lines)
{
	vector<node> proc(lines.size());
	vector<node> intersection;

	int i, j;
	string s;
	int time = 0;
	//로그데이터를 파싱하여 proc 배열에 넣는다.
	//시작과 종료를 얻는다.
	for (i = 0; i < lines.size(); i++)
	{
		//h
		s = "";
		for (j = 11; j < 13; j++)
		{
			s += lines[i][j];
		}
		time = stoi(s);

		//m
		s = "";
		for (j = 14; j < 16; j++)
		{
			s += lines[i][j];
		}
		time = time * 60 + stoi(s);

		//s
		s = "";
		for (j = 17; j < 19; j++)
		{
			s += lines[i][j];
		}
		time = time * 60 + stoi(s);

		//ss
		s = "";
		for (j = 20; j < 23; j++)
		{
			s += lines[i][j];
		}
		time = time * 1000 + stoi(s);

		proc[i].end = time;

		//during
		s = "";
		for (j = 24; lines[i][j] != 's'; j++)
		{
			s += lines[i][j];
		}
		time = stod(s) * 1000;
		proc[i].start = proc[i].end - time + 1;
	}

	int maximum = 0;
	int tmp;
	for (i = 0; i < proc.size(); i++)
	{
		tmp = 0;

		for (j = 0; j < proc.size(); j++)
		{
			//proc[i]를 기준으로 모든 proc을 검사한다.
			//(proc[i].start - 999) <= 비교 대상 <= proc[i].start
			
			if (proc[i].start - 999 <= proc[j].start && proc[j].start <= proc[i].start)
			{
				tmp++;
			}
			else if (proc[i].start - 999 <= proc[j].end && proc[j].end <= proc[i].start)
			{
				tmp++;
			}
			else if (proc[j].start <= proc[i].start - 999 && proc[i].start < proc[j].end)
			{
				tmp++;
			}
		}

		//현재 처리량 tmp와 이전의 최대 처리량 maximum을 비교하여 갱신한다.
		maximum = max(tmp, maximum);
	}

	return maximum;
}

Kakao