[2019] 후보키

문제 설명
1. 후보키 : 유일성과 최소성을 만족하는 것을 후보키(Candidate Key)라고 한다.
2. 테이블이 주어졌을 때 후보키의 최대 갯수를 구한다.
유일성(uniqueness)
릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.

최소성(minimality)
유일성을 가진 키를 구성하는 속성 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별할 때 꼭 필요한 속성들로만 구성되어야 한다.
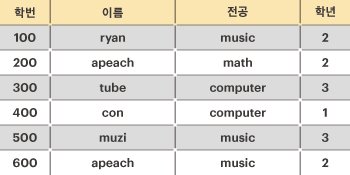
아래와 같은 경우에서 후보키는 “학번”, [“이름”, “전공”] 두 개가 된다.
문제 풀이
- 유일성을 만족시키는 키를 모두 후보키 배열에 넣어준다.
- 유일성을 만족시키는 후보키들의 최소성을 확인하여 최소성이 만족되지 않는 후보키를 제외시킨다.

#include <string>

#include <vector>

#include <algorithm>


using namespace std;

vector<vector<int>> ans;

bool is_Same(string a, string b)
{
	if (a.length() != b.length())
	{
		return false;
	}

	for (int i = 0; i < a.length(); i++)
	{
		if (a[i] != b[i])
		{
			return false;
		}
	}

	return true;
}

void dfs(vector<vector<string>>& R, int idx, vector<string> stack, int& maxi, vector<int> to_ans)
{
	//현재 키로 설정한 것이 유일한 값인지 확인
	bool can_key = true;
	for (int i = 0; i < stack.size(); i++)
	{
		for (int j = 0; j < stack.size(); j++)
		{
			if (i == j) continue;

			if (is_Same(stack[i], stack[j]))
			{
				can_key = false;
				break;
			}
		}
		if (!can_key)
		{
			break;
		}
	}

	//유일하다면 ans에 가능한 후보키를 푸시
	if (can_key)
	{
		ans.push_back(to_ans);
		return;
	}

	for (int i = idx + 1; i < maxi; i++)
	{
		for (int j = 0; j < stack.size(); j++)
		{
			stack[j] += R[j][i];
		}

		to_ans.push_back(i);
		dfs(R, i, stack, maxi, to_ans);
		to_ans.pop_back();

		for (int j = 0; j < stack.size(); j++)
		{
			for (int k = 0; k < R[j][i].length(); k++)
			{
				stack[j].pop_back();
			}
		}
	}
}

int solution(vector<vector<string>> relation)
{
	ans.clear();

	int maxi = relation[0].size();

	vector<string> stack(relation.size(), "");
	vector<int> to_ans;

	for (int j = 0; j < maxi; j++)
	{
		for (int i = 0; i < relation.size(); i++)
		{
			stack[i] = relation[i][j];
		}

		to_ans.push_back(j);
		dfs(relation, j, stack, maxi, to_ans);
		to_ans.pop_back();
	}

	//최소성을 확인한다
	int ret = 0;
	int i_idx, j_idx;
	for (int i = 0; i < ans.size(); i++)
	{
		for (int j = 0; j < ans.size(); j++)
		{
			if (i == j) continue;

			if (ans[i].size() >= ans[j].size()) continue;

			i_idx = 0;
			j_idx = 0;
			while (i_idx < ans[i].size() && j_idx < ans[j].size())
			{
				if (ans[i][i_idx] == ans[j][j_idx])
				{
					i_idx++;
					j_idx++;
				}
				else
				{
					j_idx++;
				}
			}
			if (i_idx == ans[i].size())
			{
				//j를 지운다
				ans.erase(ans.begin() + j);

				if (i < j)
				{
					j--;
				}
				else
				{
					i--;
					j--;
				}
			}
		}
	}

	ret = ans.size();

	return ret;
}

Kakao